In this post, I attempt to investigate the distribution of prime numbers and the famous Riemann hypothesis.
Categories
Author: Dr. Ikjyot Singh Kohli
Sikh, Theoretical and Mathematical Physicist, main research in the structure and dynamics of Einstein's field equations.
I wanted to test out R on Apple’s new M1/ARM architecture. Here’s how it went:
Categories
On Entropy and Time Reversal
As a huge Christopher Nolan fan, I am very excited that Tenet is finally coming out this week! Here is the new and final trailer for those of you that have not seen it yet: One of the main themes in this movie will evidently be on “time inversion/reversal” based on the reversing entropy. Since […]
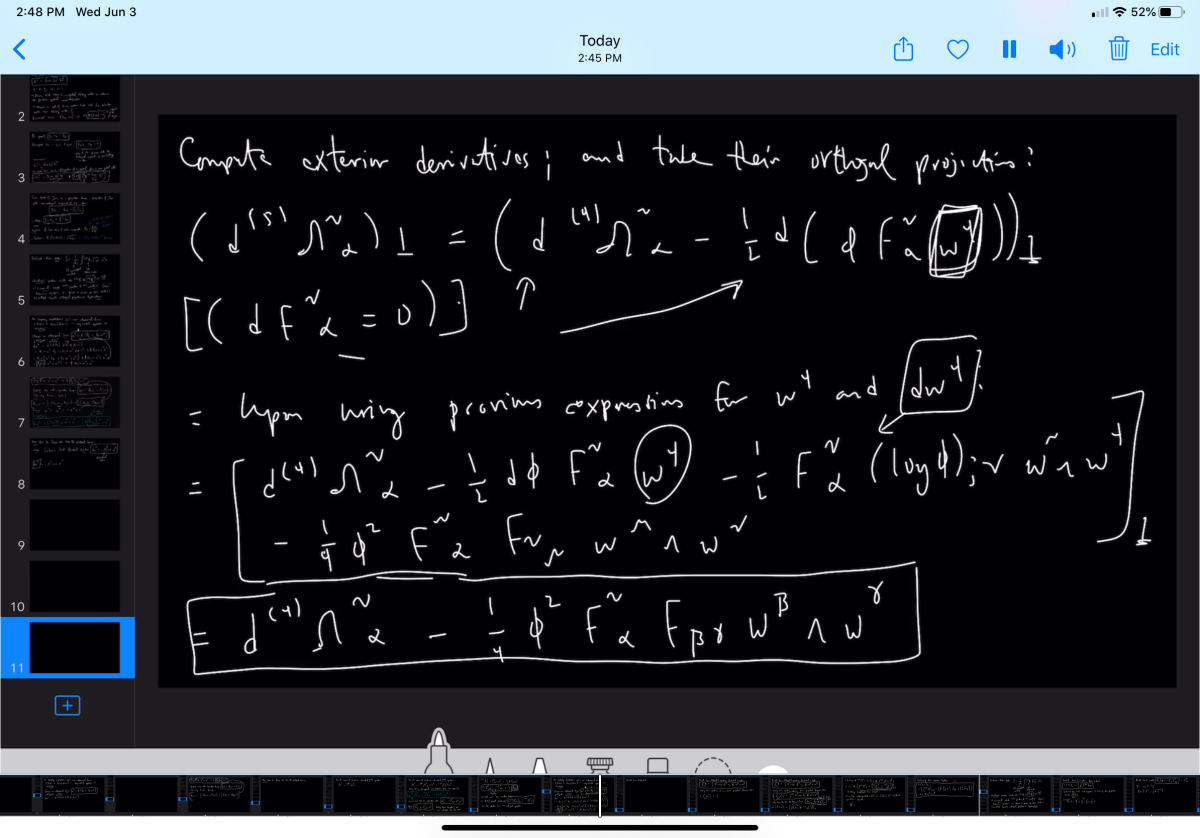
In the video below, I explain how to derive Kaluza Klein action which occurs from generalizing the Einstein-Hilbert action to five dimensions. The grand implication of this is that gravity and electromagnetism are unified!
Many textbooks when introducing ordinary least squares as a method to do regression (usually via introducing linear regression) don’t explain / derive the coefficients. Here, I explain how to do it using tensor/index notation.
Using mathematics to analyze who is a “better” player By: Dr. Ikjyot Singh Kohli It seems that nowadays one cannot escape the never-ending debate of “Who is better? Michael Jordan or Lebron James?” The situation is made worse by organizations like ESPN that have endless debates on their various shows combined with releasing lists of […]
By: Dr. Ikjyot Singh Kohli I wrote an extensive script in R that takes the most recent data available for the number of new/confirmed COVID-19 cases per day by location and computes the probability using statistical learning that a selected location will observe a new COVID-19 case (probability of observing a non-zero daily percentage return). […]
I wrote an extensive application using NLP and TensorFlow/Keras in Python that looks at all of the current and upcoming Hollywood releases for 2020 and tracks the online Twitter sentiment for each of them. The model output was then displayed in a PowerBI dashboard. In essence, we are predicting the classification probability . You can […]
By: Dr. Ikjyot Singh Kohli The conventional wisdom by the political pundits/analysts who are seeking to explain Joe Biden’s massive win in the 2020 South Carolina primary is that Jim Clyburn’s endorsement was the sole reason why Biden won. (Here is just one article describing this.) I wanted to analyze the data behind this and […]
By: Dr. Ikjyot Singh Kohli Election season is upon us again, and a number of people from political analysts to campaign advisors are making a huge deal about winning the Iowa caucuses. This seems to be the standard “wisdom”. I decided to run some analysis on the data to see if it was true. I […]
